2021-03-25

ハッシュを計算する構造体

タイトルの通りです。
衝突しにくい構造体が作りたかった（衝突すると悲しいので）

コード

struct Hash
{
  static constexpr ll M1 = (1LL << 61) - 1;
  static constexpr ll M2 = (1LL << 31) - 1;
  ll val1, val2;

  constexpr Hash(ll val = 0) noexcept
      : val1(val), val2(val) {}

  constexpr Hash(ll val1, ll val2) noexcept
      : val1(val1), val2(val2 % M2)
  {
    if (val1 >= M1)
      val1 -= M1;
  }

  constexpr Hash operator-() const noexcept
  {
    return Hash(val1 ? M1 - val1 : 0, val2 ? M2 - val2 : 0);
  }
  constexpr Hash operator+=(const Hash &h) noexcept
  {
    val1 += h.val1;
    if (val1 > M1)
      val1 -= M1;
    val2 += h.val2;
    if (val2 > M2)
      val2 -= M2;
    return *this;
  }
  constexpr Hash operator-=(const Hash &h) noexcept
  {
    val1 -= h.val1;
    if (val1 < 0)
      val1 += M1;
    val2 -= h.val2;
    if (val2 < 0)
      val2 += M2;
    return *this;
  }
  Hash operator*=(const Hash &h) noexcept
  {
    __int128 t;
    t = val1;
    t *= h.val1;
    t = (t >> 61) + (t & M1);
    if (t >= M1)
      t -= M1;
    val1 = ll(t);
    val2 *= h.val2;
    val2 = (val2 >> 31) + (val2 & M2);
    if (val2 >= M2)
      val2 -= M2;
    return *this;
  }
  constexpr Hash operator+(const Hash &h) const noexcept
  {
    return Hash(*this) += h;
  }
  constexpr Hash operator-(const Hash &h) const noexcept
  {
    return Hash(*this) -= h;
  }
  Hash operator*(const Hash &h) const noexcept
  {
    return Hash(*this) *= h;
  }
  constexpr bool operator==(const Hash &h) const noexcept
  {
    return val1 == h.val1 and val2 == h.val2;
  }
  constexpr bool operator!=(const Hash &h) const noexcept
  {
    return !(*this == h);
  }
  constexpr bool operator<(const Hash &h) const noexcept
  {
    return val1 == h.val1 ? val2 < h.val2 : val1 < h.val1;
  }
  friend ostream &operator<<(ostream &os, const Hash &h) noexcept
  {
    return os << "(" << h.val1 << ", " << h.val2 << ")";
  }
};

mod2^61-1とmod2^31-1をペアで持ってます。比較演算子<はsetとかに入れる用です。
定数倍は速いはず。

あとローリングハッシュのライブラリも作ったので置いておきます。

class RollingHash
{
  Hash B;
  pair<Hash, Hash> _calc(string &s, int l, int r)
  {
    assert(l <= r);
    Hash res, p = 1;
    for (int i = r - 1; i >= l; i--)
    {
      res += p * ll(s[i]);
      if (i != l)
        p *= B;
    }
    return {res, p};
  }

public:
  RollingHash()
  {
    random_device seed;
    mt19937 engine(seed());
    B = Hash(ll(engine()) + 1000, ll((engine()) + 1000));
  }

  // [l, r) のハッシュを計算
  Hash calc(string &s, int l = -1, int r = -1)
  {
    if (l == -1)
      l = 0, r = s.length();
    return _calc(s, l, r).first;
  }

  // s の長さ m の部分文字列のハッシュ
  vector<Hash> Roll(string &s, int m)
  {
    vector<Hash> hash;
    int n = s.length();
    assert(n >= m);
    hash.resize(n - m + 1);
    auto [h, p] = _calc(s, 0, m);
    hash[0] = h;
    for (int i = m; i < n; i++)
    {
      h -= p * ll(s[i - m]);
      h *= B;
      h += ll(s[i]);
      hash[i - m + 1] = h;
    }
    return hash;
  }
};

機能が少ないのでもう少し整備したい

Verify

ABC141E - Who Says a Pun?

Submission #21243369 - AtCoder Beginner Contest 141

参考

安全で爆速なRollingHashの話 - Qiita

「1000000007 で割ったあまり」の求め方を総特集！〜逆元から離散対数まで〜 - Qiita

2020-12-11

素数判定アルゴリズムについて

この記事はCCS Advent Calendar 2020の11日目の記事として作成されました。

前の記事：
note.com

nullです。今回は素数判定や素因数分解を行うアルゴリズムについて色々書きます。

整数 $N$ の素数判定

最も初歩的なものとしては、 $2$ 以上 $N-1$ 以下の整数が $N$ を割り切るかどうか調べる、という方法が考えられます。
例えばC++での実装は以下のようになります。

#include <iostream>

int main()
{
  long long n;
  std::cin >> n;
  if (n <= 1)
  {
    std::cout << n << " is not prime.\n";
    return 0;
  }
  bool is_prime = true;
  for (long long i = 2; i <= n - 1; i++)
  {
    if (n % i == 0)
    {
      is_prime = false;
      break;
    }
  }
  if (is_prime)
    std::cout << n << " is prime.\n";
  else
    std::cout << n << " is not prime.\n";
}

このコードは最大で $N-2$ 個の候補について探索を行うため、（時間）計算量 $O(N)$ のコードといえます。
計算量とは、「あるアルゴリズムの効率がどれだけ優れているか」を表す指標です。この場合であれば探索の回数が大体 $N$ に比例することを意味しています。

C++であれば1秒に $10^9$ 回程度のループを回せるので、このコードでは $N \leq 10^9$ 程度であれば現実的な時間で素数判定が出来ます。

しかし $N$ がこれより大きい場合には途方もない時間がかかってしまいます。もっと効率のよい方法はないでしょうか。

$N \geq 2$ が合成数であることは、 $N = A \times B \ (A,B \geq 2)$ と2つの2以上の整数の積に分解できることと同値です。
ここで重要な考察として、 ${\rm min}(A,B) \leq \sqrt{N}$ が成り立ちます。
よって実は、 $2$ 以上 $\lfloor \sqrt{N} \rfloor$ 以下の整数が $N$ を割り切るかどうか調べるだけで十分であるとわかります。

#include <iostream>

int main()
{
  long long n;
  std::cin >> n;
  if (n <= 1)
  {
    std::cout << n << " is not prime.\n";
    return 0;
  }
  bool is_prime = true;
  for (long long i = 2; i * i <= n; i++)
  {
    if (n % i == 0)
    {
      is_prime = false;
      break;
    }
  }
  if (is_prime)
    std::cout << n << " is prime.\n";
  else
    std::cout << n << " is not prime.\n";
}

このコードの計算量は $O(\sqrt{N})$ であるため、 $N \leq 10^{18}$ 程度であれば判定できます。 $N$ の上限が先程の $10^9 = 1000000000$ 倍になりました！
このように計算量のよいアルゴリズムを考えることで、規模の大きい問題を現実的な時間で解くことが出来ます。

整数 $N_1, N_2, \dots, N_k$ の素数判定

今度は複数の整数の素数判定を行う場合を考えます。もちろん一つ一つの整数に対して先程のアルゴリズムを適用してもよいのですが、このような場合には、ある種の「前計算」を行うことで全体での判定効率がアップします。

${\rm max} N_i = M$ として、 $M$ 以下の素数を列挙したとしましょう。その場合、列挙した素数の中に $N_i$ が含まれるかどうかを調べるだけでよいので、各判定を $O(1)$ で行えます。魅力的ですね。

問題はどうやって素数を列挙するかですが、これを上手く実現するアルゴリズムとして、エラトステネスの篩が知られています。
$i = 2,3,\dots,M$ の順に、もし $i$ が素数（＝まだ消されていない）ならば $i$ を素数と確定した上で $2i,3i,\dots$ を消し、素数でない（＝既に消されている）ならば何もしない、という操作をすることで素数を列挙することが出来ます。

このアルゴリズムの計算量は $O(M \ {\rm log}{\rm log} M)$ であることが知られています。*1
このように、前計算を行うことで各判定を効率よく行うことが出来ます。

#include <iostream>

const int MAX_N = 1e7;
bool is_prime[MAX_N + 1];

void make_primes()
{
  std::fill(is_prime, is_prime + MAX_N + 1, true);
  for (int i = 2; i <= MAX_N; i++)
  {
    // 既に消されている場合はスルー
    if (!is_prime[i])
      continue;
    // i の倍数を消す
    for (int j = i + i; j <= MAX_N; j += i)
      is_prime[j] = false;
  }
}

int main()
{
  make_primes(); // 素数を前計算
  int n;
  while (std::cin >> n)
  {
    if (n >= 2 and is_prime[n])
      std::cout << n << " is prime.\n";
    else
      std::cout << n << " is not prime.\n";
  }
}

$N$ の素因数分解

一般に、巨大な数の素因数分解は非常に困難な問題とされています。
しかし、そこそこの大きさの数であれば、現実的な時間で素因数分解を行うことが可能です。

エラトステネスの篩を拡張してみましょう。
数を消す代わりに、その数が何で割り切れるかを記録することにします。そうすると前計算の計算量は変わらないまま、素因数分解を行うことができます。
再帰的に、 $N$ が素数でなければ $N$ を先程記録した数で割って同様の操作を繰り返すことで、素因数分解が行えます。

$N$ の素因数の個数は最大でも ${\rm log}_2 N$ 個程度であるため、計算量は $O({\rm log} N)$ です。
ただし実装の際は連想配列std::mapを用いているため、素因数分解の計算量は $O({\rm log^2} N)$ となっています。（std::unordered_mapを使うとならし $O({\rm log} N)$ になります）

#include <iostream>
#include <map>

const int MAX_N = 1e7;
int can_div[MAX_N + 1] = {}; // iを割り切る2以上i未満の素数（なければ0）

void make_primes()
{
  for (int i = 2; i <= MAX_N; i++)
  {
    // 既に消されている場合はスルー
    if (can_div[i] != 0)
      continue;
    // i の倍数を消す
    for (int j = i + i; j <= MAX_N; j += i)
      can_div[j] = i;
  }
}

// nの素因数分解
std::map<int, int> factorization(int n)
{
  if (can_div[n] == 0)
  {
    std::map<int, int> mp;
    mp[n] = 1;
    return mp;
  }
  std::map<int, int> mp = factorization(n / can_div[n]);
  mp[can_div[n]]++;
  return mp;
}

int main()
{
  make_primes(); // 素数を前計算
  int n;
  while (std::cin >> n)
  {
    std::cout << n << " = ";
    std::map<int, int> mp = factorization(n);
    for (auto itr = mp.begin(); itr != mp.end(); itr++)
    {
      auto [p, e] = *itr;
      std::cout << p << "^" << e;
      if (next(itr) != mp.end())
        std::cout << " * ";
      else
        std::cout << "\n";
    }
  }
}

素数判定の確率的アルゴリズム

世の中には、「100%ではないが、十分な確率で正しい解が求まる」アルゴリズムがあります。これを確率的アルゴリズムといいます。
素数判定を行う確率的アルゴリズムのうち代表的なものは2つあり、フェルマーテストとミラーラビン素数判定法です。

フェルマーテストは、フェルマーの小定理を利用した判定法です。フェルマーの小定理は、 $p$ が素数かつ $a$ と $p$ が互いに素のときに $a^{p-1} \equiv 1 \ ({\rm mod} \ p)$ が成り立つというものです。

$N$ をフェルマーテストで素数判定する流れは次のようになります。

まず、 $2$ 以上 $N-1$ 以下の整数 $a$ をランダムに選びます。
もし $a$ と $N$ が互いに素でないならば、 $a$ と $N$ は $2$ 以上 $N-1$ 以下の公約数を持つので、その時点で $N$ は素数ではありません。
互いに素な場合は、もし $N$ が素数ならフェルマーの小定理より $a^{N-1} \equiv 1 \ ({\rm mod} \ N)$ が成り立つはずです。よってこれが成り立たなければ素数ではありません。

$N$ が素数かもしれない場合は、再び整数 $a$ をランダムに選びます。これを十分な回数繰り返します。

このテストはあくまでも $N$ が素数であるための必要条件を調べているだけにすぎないので、正しい判定ができるとは限りません。しかし実際にはそれなりの確率で素数判定ができることが知られています。*2一方でカーマイケル数と呼ばれる合成数に対しては、どのような $a$ を選んでも素数と判定されてしまうという問題点があります。

ミラーラビン素数判定法は、フェルマーテストを改善した、より高い確率で正しい素数判定を行える判定法です。フェルマーテストと違ってカーマイケル数に対しても高確率で正しい判定を行うことができます。ここでは名前を紹介する程度にとどめておきます。（自分もよくわかってないので）

おわりに

素数に関するアルゴリズムの研究は古くからなされているだけあって、とても奥が深いです。現在も盛んに研究がなされています。興味を持った方は是非調べてみてください。
また、計算量のよいアルゴリズムを見つけるということの大切さが伝わればよいなと思っています。これはゲーム制作やアプリ開発など、どの分野でも有用だと思います。

おまけ

なんかめっちゃ堅苦しくなっちゃったので家にあるぬいぐるみの写真載せときます

f:id:null_mn:20201209070637j:plain
f:id:null_mn:20201209070734j:plain
f:id:null_mn:20201209070659j:plain
f:id:null_mn:20201209070647j:plain
f:id:null_mn:20201209070625j:plain
f:id:null_mn:20201209070723j:plain
f:id:null_mn:20201209070711j:plain
f:id:null_mn:20201209070747j:plain *3
f:id:null_mn:20201209070800j:plain *4

*1:エラトステネスのふるいとその計算量 | 高校数学の美しい物語

*2:1回のテストでカーマイケル数以外の合成数を1/2ほどふるい落とせるようです。

*3:ゲーミング魔剤

*4:オリジナル魔剤

2020-12-05

Advent Calendar Contest 2020 D - Rotate and Accumulate

yukicoderのAdvent Calendar Contest 2020のD問題を作問しました。

問題

yukicoder.me

解法

解説を見てください。（おわり）

余談

自分の中ではド典型だと思ってたので没にするか迷いましたが、Testerに後押しされたので出題することとなりました。大正解だったと思います。Testerのkeymoonさん、ありがとうございました。あと一瞬自作問題全部自明に見える期が来て★3に落としましたが、流石に違和感あったので★3.5に戻しました。危なかったです。

余談ですが、TLの見積もりを誤ったせいで、限界定数倍高速化した $O(NQ)$ が通るらしいです。びっくり。さらに $r_i$ の度数分布表を作ると $O(N^2)$ になって、高速化すると1.5sとかになるみたいです。びっくり。

感想

犯罪には気を付けよう！

2020-11-23

AtCoder黄色になりました

先日のABC184でついに入黄しました！

AtCoder黄色になりました！！ pic.twitter.com/VMPiKQFLvo
— stoq (@stoq_) 2020年11月22日

青になってから約1年のタイミングで色変できてうれしいです。慣例に倣って色変までにやったことを書きます。

アルゴリズムやデータ構造について

よく使ったもの

・BIT(Fenwick Tree)

・セグメントツリー（遅延評価含む）

・その他基本的なデータ構造

時々使ったもの

・FFT, NTT

・HLD

・Trie木

・ローリングハッシュ

・掃き出し法

・Mo

あまり使わなかったもの

・Suffix Array

・最大流、最小費用流（やった方がよさそう……）

・その他発展的なアルゴリズム、データ構造

ICPCに向けた精進

ICPC国内予選の対策として、重実装や幾何の対策を重点的に行いました。そのおかげでABC181で幾何を早解きして成功するなどの成果がありました。「この分野では負けない！」みたいな分野を作っておくと自信が保てるのでオススメです。

過去問埋めもAtCoderに限らず、Codeforces, AOJ-ICPC, yukicoder, JOI, yosupo judgeなどを埋めると総合的な力がつきます。

解説をたくさん見る

解説を見るべきか見ないべきかは人によりますが、個人的には方針がすぐに立たない問題は解説を見た方がいいと思っています。また、公式解説だけでなく有志のブログも読んだ方がいいです。公式解説が意味不明でも、実際に通している人の解法は典型テクニックの積み重ねであることが多いです。

さらに一度解いた問題を時々ランダムに開いてみて、解法が浮かんでくるかを試してみるのも復習効果があります。わからない場合は再び解説をよく読むとよいです。

Educational Codeforces Roundバチャ

Educational Codeforces Round、通称えでゅふぉは、教育的と謳っているだけあって典型テクの学びが多く得られます。バーチャル参加をお勧めします。（たまに変な問題もありますが……）

飽きた場合は放置してみる

一時期競プロから離れて音ゲーばっかやってましたが、しばらくするとモチベが戻りました。やる気が出ない場合はやる気が出るのを待ちましょう。

作問する

AtCoder青の期間中に、yukicoderで2回セット出題をしました。作問をすると作問者の気持ちがわかる他、題材となるアルゴリズムに詳しくなるなどのメリットがあります。あと純粋に楽しいです。みんなも作問やろう！

おわりに

競プロを始めたときは自分が黄色になれると思っていなかったのでとても嬉しいです。

AtCoder橙はまだまだ遠いですが行けるところまで行きます。次はCodeforces濃橙を目指します。

2020-11-07

ICPC2020国内予選参加記

ICPC国内予選に参加したので参加記を書きます。

メンバーははにゅさん、ももはらさん、僕(stoq)のチームharaharaです。（いつもの）

開始前

方眼ノートを買ったり、ネットの海からライブラリを拝借したり、三度寝したりしました。

コンテスト

最初問題が見れないトラブルがあってはらはらしましたが、10分後くらいに見えるようになりました。

ももはらさんがA、はにゅさんがB、僕がCを開きました。結果的に問題の相性が最高だったと思います。

Cは数学問で、正の整数 $a,b,c$ が $a \times b \times c = p \ (1 \leq p \leq 10^{15})$ を満たすときの $a+b+c$ の最小値を求める問題でした。素因数分解とDFSを書いて実行すると定数倍が大きく30秒くらいかかったものの、提出して無事AC。この時点で予選通過確定してたっぽい？あといつの間にかABも通ってました。（すごい）

Eが解けそうなので睨むものの、単純なDPでは解けそうにないとわかりはにゅさんと考え込みます。グラフの問題っぽい？考察をしているとももはらさんが構文解析のDを通したとの連絡が。最強。その後はももはらさんがE、はにゅさんがF、僕がHを考えることに。Hはガチめの幾何で、どうせ下に凸だからと三分探索をやると、終盤で実は凸じゃないことが発覚して悲しくなりました。Fは愚直を書いたみたいですが謎のWAでだめだったようです。そんなこんなでコンテストが終了しました。

結果

f:id:null_mn:20201107002246p:plain
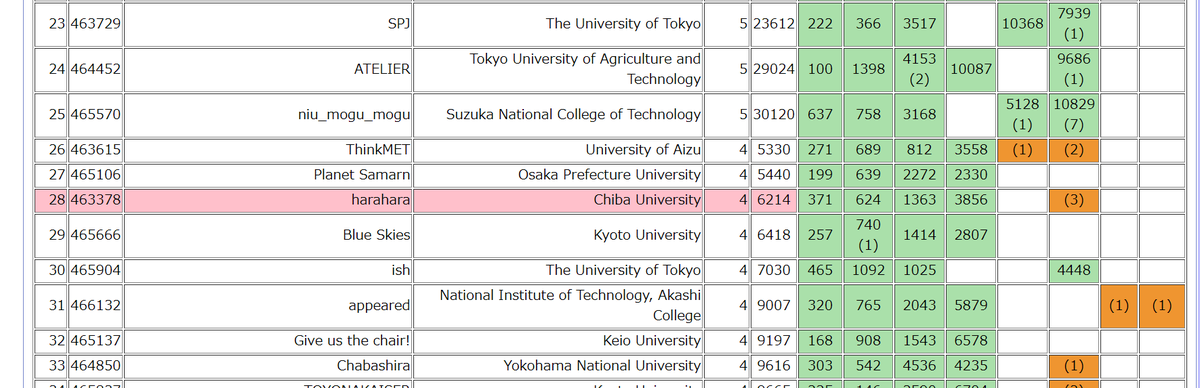
4完28位で予選突破しました！
今回はEが難しめだったので、前半の速解きが成功したのが大きかったと思います。
横浜大会ではもっと良い成績を残したいです。

おわりに

ICPCは起床コンテスト。

2020-10-30

ARC106-D Powers を直感的に解く

今更ですが、ARC106-D Powers の簡単な解説を書きます。

問題リンク：

atcoder.jp

問題概要：

長さ $N$ の数列 $\{A_i\}$ がある。 $1 \leq X \leq K$ それぞれについて、

$\displaystyle{ \left( \sum_{i \lt j} (A_i+A_j)^X \right) \ {\rm mod} \ 998244353 }$
を求めよ。
$1 \leq N \leq 2 \times 10^5$
$1 \leq K \leq 300$
$1 \leq A_i \leq 10^8$

解法：

対称性から $\displaystyle{\sum_{i \lt j} (A_i+A_j)^X = \frac{1}{2} \sum_{i \neq j} (A_i+A_j)^X}$ なので、これを求めます。（こちらの方が後の計算が楽です。）
まず括弧の中を展開すると、

$\begin{aligned} \sum_{i \neq j} (A_i+A_j)^X &= \sum_{i \neq j} \left(\binom{X}{0} A_i^X + \binom{X}{1} A_i^{X-1} A_j + \cdots + \binom{X}{X} A_j^X \right) \\ &= \binom{X}{0} \sum_{i \neq j} A_i^X + \binom{X}{1} \sum_{i \neq j} A_i^{X-1} A_j + \cdots +\binom{X}{X} \sum_{i \neq j} A_j^X \end{aligned}$

となります。
二項係数は高速に前計算できるので、 $\displaystyle{ \sum_{i \neq j} A_i^k A_j^l \ (0 \leq k,l \leq K)}$ が高速に求まればよいです。

突然ですが、次のような長方形を考えてみましょう。

f:id:null_mn:20201030061131p:plain

すると、 $\displaystyle{ \sum_{i \neq j} A_i^k A_j^l}$ は次の赤い部分の面積に一致します。

f:id:null_mn:20201030061029p:plain

これは次の（緑の面積）-（青の面積）で求まります。

f:id:null_mn:20201030061149p:plain

f:id:null_mn:20201030061141p:plain

緑の面積は $(A_1^k + \cdots + A_N^k)(A_1^l + \cdots A_N^l)$ 、青の面積は $A_1^k A_1^l + \cdots + A_N^k A_N^l$ で求まるので、
$\displaystyle{ \sum_{i \neq j} A_i^k A_j^l = \sum_{i} A_i^k \sum_{i} A_i^l - \sum_{i} A_i^{k+l}}$
が成り立つとわかります。

よって、 $0 \leq k \leq K$ に対し $\displaystyle{\sum_{i} A_i ^k}$ を前計算しておくことで $\displaystyle{ \sum_{i \neq j} A_i^k A_j^l}$ が求まり、最初の式の値も求まります。

このように二重和が登場する場面では、分割された長方形の面積を考えることで式変形を直感的に行える場合がしばしばあります。
式変形自体は特に目新しいものではないですが、「直感的にわかる」ことは発想を得る上で重要だと思うので、是非役立ててみてください。

2020-10-26

ICPC2020模擬国内　参加記

いつも通りstoq, momohara, hanyuのチームharaharaで模擬国内2020に参加しました。

覚えてる範囲で書きます。

開始前

30分前に起床する（すいません）。ごはんを食べ損ねる。TLを見るとももはらさんも同じことやってた。

A～Cの割り振りを決める。いつも大体同じ

コンテスト

ももはらさんがA、はにゅさんがB、僕がCを開く。しばらくしてA, Bが通る。

Cがなかなか解けずかなり焦る。忍小宮って誰？ようやくそれっぽいコードがかけたものの、出力ファイルを覗くと個数が負になってたのでデバッグする。かなり時間をかけてAC。ここまでで1時間ちょっと。

Fの考察に取り掛かっている間にはにゅさんが2-SATを書いて $O(N^3)$ でEを通す。すごい。

その後ももはらさんがDで苦戦してたっぽいのでコードを見る。よくわかりませんでした（ごめんなさい）。少ししてからDが通る。すごい。ここまでで2時間くらい。

順位表を見るとF, Gが不可能そうなのでHを見る。許容誤差 $10^{-10}$ で二度見した。ループがあるとき0、ないとき-1/mを出力するコードを書いたらサンプルが合ったけど流石に通らなかった。そうこうしているうちにコンテストが終了する。

結果

f:id:null_mn:20201026011208p:plain

5完で全体24位でした！チームメイトが強くてとても助かりました。感謝....…

ライバルチームのstate_of_the_artに数十秒差で負けたのがちょっと悔しいですが、十分な順位を取れたので満足です。予選本番は20位以内を目指します。

おわりに

寝坊には気を付けましょう。

コード

Verify

ABC141E - Who Says a Pun?

参考

整数 の素数判定

整数 の素数判定

の素因数分解

素数判定の確率的アルゴリズム

おわりに

おまけ

問題

解法

余談

感想

アルゴリズムやデータ構造について

よく使ったもの

時々使ったもの

あまり使わなかったもの

ICPCに向けた精進

解説をたくさん見る

Educational Codeforces Roundバチャ

飽きた場合は放置してみる

作問する

おわりに

開始前

コンテスト

結果

おわりに

問題リンク：

問題概要：

解法：

開始前

コンテスト

結果

おわりに

整数 $N$ の素数判定

整数 $N_1, N_2, \dots, N_k$ の素数判定

$N$ の素因数分解